I recently pushed an update to my statistical bootstrapping package for Go. This introduces a PresampledResampler, which precomputes the sampled indices ahead of time.

Here’s a subset of what bootstrapping involves if you’re not familiar with it:

1. You start with an initial sample. Let’s say it’s an array of 1000 numbers.
2. You randomly pick 1000 values from this initial sample with replacement (i.e. duplicates are fine). You now have a second 1000-value sample.
3. Repeat step 2 a bunch of times.

Random number generation for step 2 can be expensive. Even if you’re using a pseudo-random number generator, there’s a bunch of operations involved to generate the next value. For the purposes of bootstrapping, it’s probably fine to use the same random numbers because you’ll have enough variation with the generated samples.

My precomputation just generates a bunch of random numbers ahead of time and reuses them. How does this “presampling” affect performance?

$ go test -cover -test.bench=.* -benchmem
BenchmarkResampler-4             	  100000	     19976 ns/op	      46 B/op	       0 allocs/op
BenchmarkPresampledResampler-4   	  500000	      3242 ns/op	      46 B/op	       0 allocs/op
PASS
coverage: 100.0% of statements
ok  	github.com/Preetam/bootstrap	16.519s

It’s over 6 times faster. Neat!

Matrix multiplication

Here’s another optimization that works if your sample aggregation is summation. That means every time you have a 1000-value sample like in the initial example, you just calculate its sum. If you resample N times, you’ll end up with N 1000-value samples, and N sums. You can then compare your initial sum with the N generated ones.

If you precompute the sampled indices, you’ll have N 1000-value arrays with random indices. If we assume that all of our samples have 1000 elements, we can encode that information a little differently. Instead of storing random indices, we can instead store the number of times the value at that index contributes. For example, if the first value shows up twice, we’ll store 2 in index 0 instead of storing 0 in two locations. You can then arrange N of these “weights” arrays into a matrix.

The cool thing about this approach is that the bootstrapping process ends up being matrix multiplication.

  Original        Weights    Resampled
   sample         matrix        sums
[ 1 x 1000 ] × [          ] = [ 1 x N ]
               [          ]
               [          ]
               [ 1000 x N ]
               [          ]
               [          ]
               [          ]

Matrix multiplication is something that can be made really fast with SIMD and/or GPUs.

Here’s a great slide deck I found about this sort of stuff:

https://on-demand.gputechconf.com/gtc/2013/presentations/S3338-Bootstrap-Statistics-Simulation.pdf

Some screenshots from that…

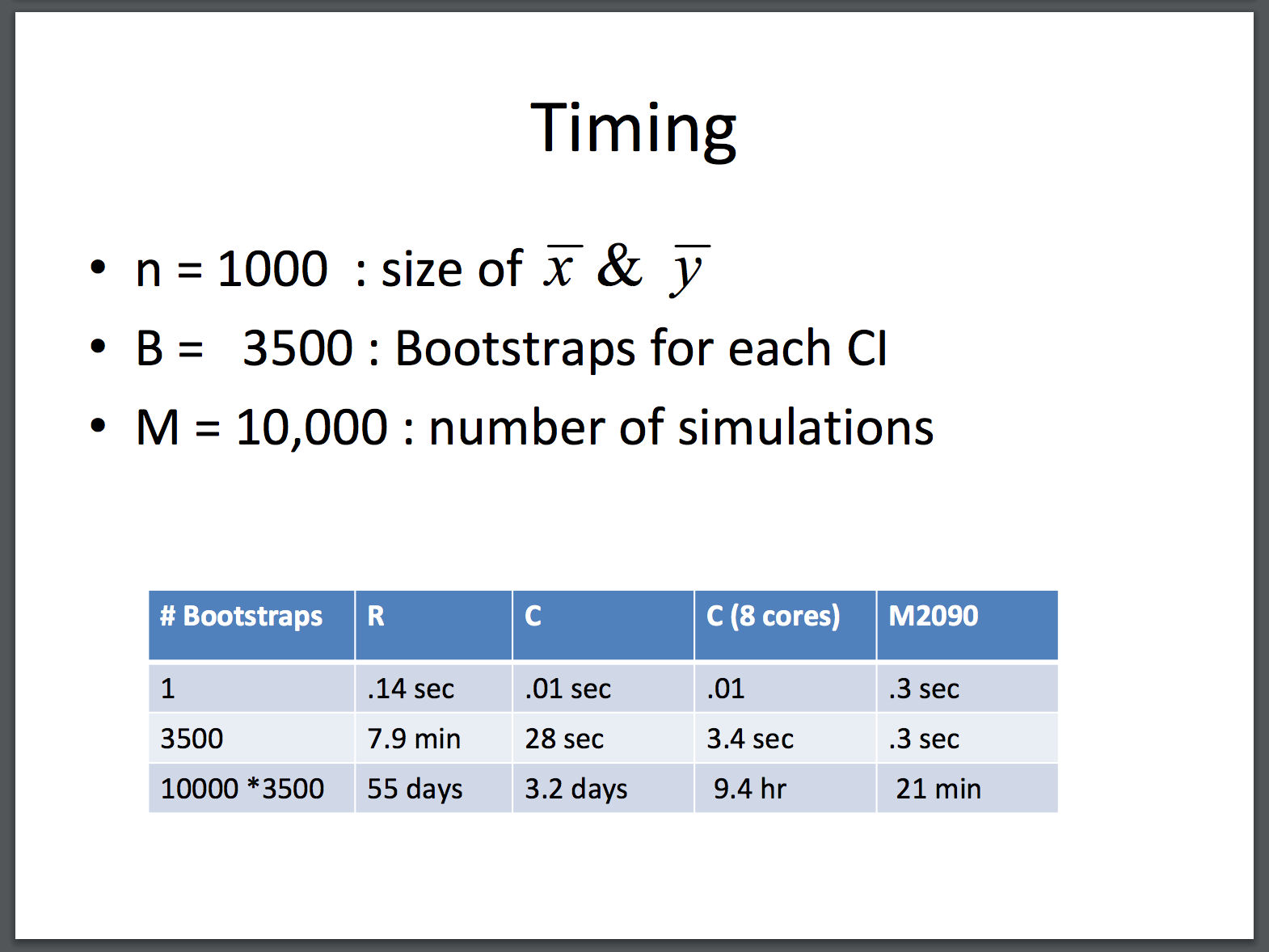
M2090 is a GPU. I should try out one of those AWS GPU instances 🤔.